Полет мяча

полет мяча

Почему же игрока постигла неудача? Что здесь виной — волнение, усталость, излишняя поспешность? Или, может быть, неровность поля? Так или иначе, нападающий допустил неточность в технике выполнения удара.

А нельзя ли установить, в чем заключалась эта неточность? Или, если задать вопрос иначе, — как должен был игрок в данном случае произвести удар, чтобы он был правильным, прицельным по высоте?

Для того, чтобы ответить на этот вопрос, надо, прежде всего, знать закономерности полета футбольного мяча.

Вспомним всегда волнующее начало футбольного состязания. Свисток судьи, и неподвижно лежавший в центре поля мяч приходит в движение. Он то катится по земле, то описывает в воздухе самые разнообразные линии, порой весьма неожиданные.

Отчего же зависит каждая линия или, как принято ее называть, траектория полета мяча?

— От силы и направления удара, — так, очевидно, скажут многие.

Этот ответ правилен, но лишь частично.

Мяч приходит в движение действительно в результате Силового воздействия игрока, то есть удара, при котором на мяч действует значительная сила в течение очень малого промежутка времени (тысячных долей секунды). Кстати говоря, остановка мяча игроком, игра головой, отскок мяча от поверхности поля — все это, по сути, явления удара.

Однако траектория полета мяча зависит не только от силы и направления удара, но и от тех сил, которые дополнительно действуют на мяч в полете — силы тяжести или веса, силы сопротивления воздуха и т. д.

Чтобы лучше усвоить это, рассмотрим простейший случай, когда мяч отвесно падает с некоторой высоты. Допустим сначала, что это происходит не в воздушной среде, а в пустоте и что начальная скорость мяча равна нулю.

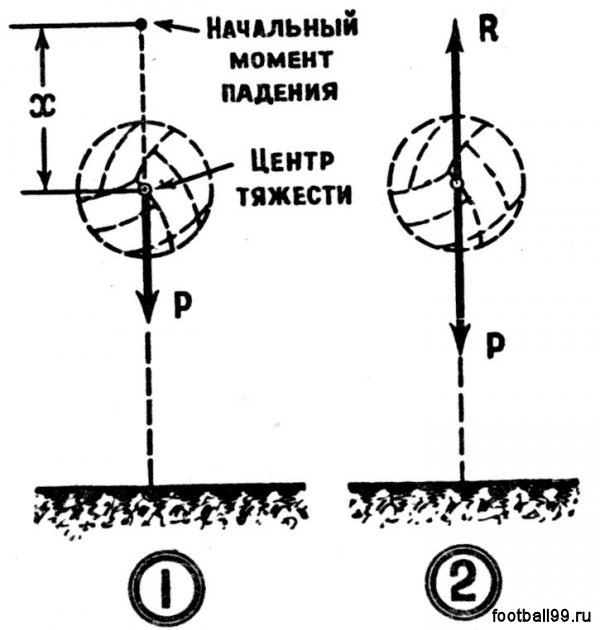
Какие же силы заставляют мяч двигаться в данном случае? Только одна — сила тяжести Р (рис. 1). А с какой скоростью летит мяч? Мы знаем, что все тела падают в пустоте с постоянным ускорением (§), равным 9,8 м/сек. Следовательно, мяч, как и любое тело, падая в безвоздушном пространстве, движется равномерно-ускоренно. Между расстоянием (*), временем (I) и скоростью (V) существуют определенные зависимости. Они выражаются формулами, известными читателю еще из школьного курса физики. Эти формулы понадобятся нам, когда мы будем составлять графики движения мяча в пустоте и в воздухе.

Каждый из нас по собственному опыту знает, как трудно идти, а тем более бежать по дну реки даже в мелкой воде. Это объясняется силой сопротивления воды. Аналогичное явление происходит, когда мяч движется в воздухе.

Здесь на падающий мяч помимо веса (Р) действует и сила сопротивления воздуха (Р), противоположная направлению скорости (рис. 2). Поэтому скорость падения мяча в воздухе всегда меньше скорости падения в пустоте. Сила сопротивления воздуха зависит от многого: от скорости и формы тела; от площади его поперечного сечения, перпендикулярного направлению движения; наконец, от плотности воздуха.

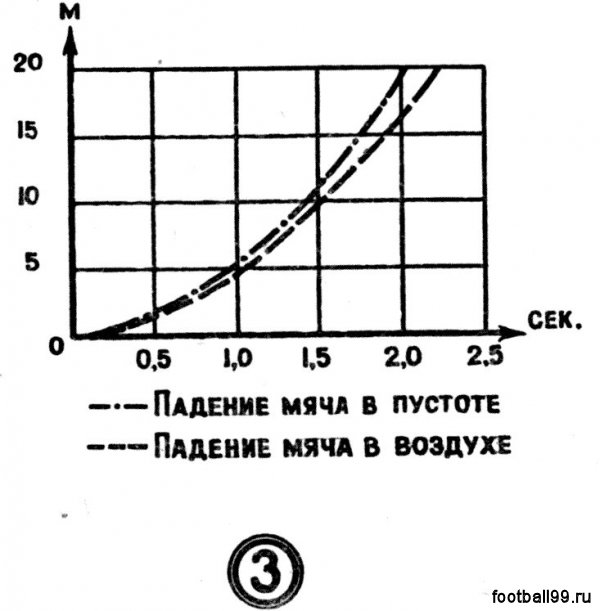
Скорость падения мяча в воздухе интенсивно растет в течение первых 2—2,5 секунды. Затем она увеличивается медленнее, приближаясь к предельной скорости, равной 18,4 м/сек. Расчет показывает, что скорость, близкую к указанной, мяч приобретает за 5,5 секунды падения.

Но так как в игре мяч редко поднимается выше 15 метров, то практически максимальную скорость падения мяча

можно принять равной 14 м/сек. Она мало отличается от скорости падения в пустоте. Это очень важно, так как во всех расчетах, связанных с вертикальным падением мяча, можно с достаточной точностью пользоваться графиками падения в пустоте, которые строятся очень просто.

Среди футболистов при разборе тактических ситуаций часто возникают споры. Это естественно, так как- многие тактические задачи могут иметь несколько решений. Однако наиболее рациональным будет все-таки одно!

Решим, например, такую задачу: должен ли вратарь выйти из ворот на игру в тот момент, когда мяч начинает падать с пятиметровой высоты на нападающего, который находится в положении, выгодном для удара по воротам?

Условимся, что мяч находится в 10 метрах от ворот, а вратарь может пробежать десятиметровое расстояние за 1,4 секунды.

Вот теперь нам и помогут графики пути мяча, падающего в пустоте и в воздухе (рис. 3). По этим графикам нетрудно установить, что мяч пролетит пятиметровое расстояние до поля за 1 секунду, а до головы нападающего — еще скорее. Вратарь в этом случае наверняка опоздает. Нерасчетливо покинув ворота, он будет в пути в тот момент, когда нападающий уже сможет сыграть головой.

Отсюда ответ на поставленный в задаче вопрос: в игру должен включиться не вратарь, а защитник.

Здесь приведен, конечно, простейший пример. Но и во многих других случаях правильный ответ можно получить с помощью такого же анализа.

— Позвольте! — возразят нам.— Вратарь не в состоянии защищать ворота, держа в руках графики и расчеты!

Никаких чертежей у игроков на поле, разумеется, нет и быть не может. Однако, решая подобные задачи за столом и выполняя простейшие расчеты, игроки безусловно научатся быстрее и более сознательно находить правильные решения и в игровых ситуациях.

Вернемся теперь к вопросу, поставленному в начале статьи: как добиться точности ударов по воротам — их прицельности по высоте?

Представим себе, что мяч, находившийся на поверхности поля, приобрел в результате удара некоторую начальную скорость. Разумеется, во время полета скорость будет непрерывно меняться.

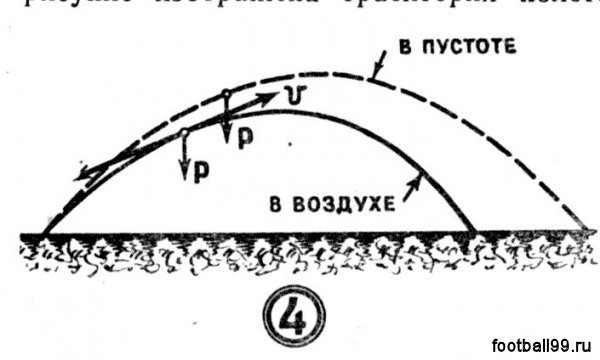
Если бы мяч двигался в пустоте, на него действовала бы только сила тяжести (Р), направленная вертикально вниз. Под действием этой силь: мяч перемещался бы по кривой линии — параболе, как это показано на рис. 4. На том же рисунке изображена траектория полета

мяча в воздухе (угол вылета и начальная скорость одинаковы в обоих случаях). Траектория полета мяча в воздухе будет также криволинейной, но более крутой.

Сравнивая траектории, легко заметить, что мяч в воздухе поднимается не так высоко, как в пустоте. Дальность его полета тоже меньше. При движении в пустоте скорость мяча в момент падения равна начальной скорости, а при движении в воздухе она меньше скорости вылета.

Объясняется это явление просто. При полете в воздухе мяч. помимо силы тяжести (Р), испытывает воздействие и силы сопротивления воздуха (/?), направленной противоположно скорости.

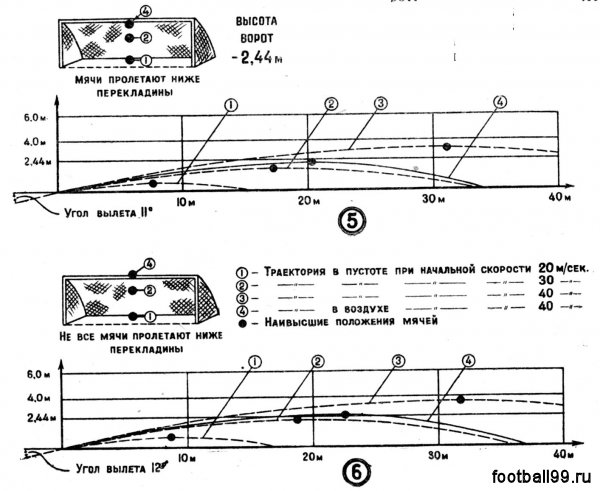
Начальная скорость и угол вылета оказывают решающее влияние на дальность полета и максимальную высоту мяча. Каким же должен быть наибольший угол вылета, чтобы удар по воротам был прицельным по высоте? Другими словами, каким должен быть этот угол, чтобы максимальная высота полета мяча не превышала высоты ворот — 2,44 метра? У

Посмотрите на рис. 5. Здесь показаны траектории движения мяча в пустоте и в воздухе при угле вылета 11° и при начальных скоростях 20, 30 и 40 м/сек. Учтите, что, не вычислив теоретически траекторию в пустоте, нельзя рассчитать и путь мяча в воздухе.

На рисунке видно, что при начальной скорости мяча 40 м/сек. максимальная высота траектории полета мяча в воздухе не превышает 2,44 метра. Значит, даже при такой большой скорости угол вылета, не превышающий 11°, обеспечит прицельность ударов по высоте.

Траектории при угле вылета, равном 12°, показаны на рис. 6. Кривая полета мяча в воздухе показывает, что начальная скорость 40 м/сек. уже не удовлетворит условиям прицельности — мяч пройдет выше ворот. А разница в углах вылета составляет всего один градус!

В нашем анализе мы исходили из того, что удары по воротам дают мячу начальную скорость в пределах 20—40 м/сек. Поэтому футболист должен твердо знать, что при ударе практически с любого расстояния угол вылета, не превышающий 11°, гарантирует прицельность — мяч выше перекладины не поднимется.

Ответили ли мы на вопрос о причине неудачи нападающего?

Нет, еще не совсем. Нами доказано, что угол вылета мяча оказался слишком большим. Мы установили, каким он примерно должен быть. Но теперь вопрос об угле вылета надо связать с техникой выполнения удара.

Для примера рассмотрим удар серединой подъема, наиболее эффективный по прицельности.

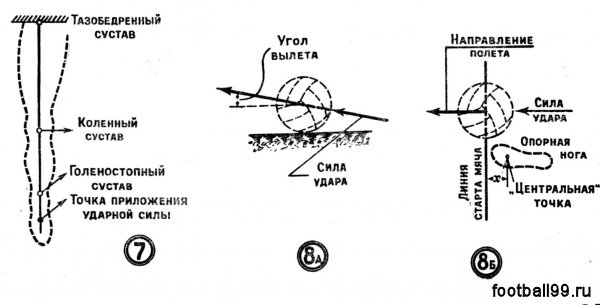
Как производится сильный удар? Бьющая нога в момент удара выпрямлена в коленном суставе до отказа. Ступня также отведена до отказа, и вся нога напряжена. Если посмотреть на бьющую ногу спереди и представить ступню, голень и бедро в виде отрезков прямой, мы увидим, что все эти отрезки расположены на одной прямой линии (рис. 7).

В момент удара игрок приподнимается на носок опорной ноги. При этом носок бьющей ноги проходит над поверхностью поля, не задевая ее (это предохраняет голеностопный сустав от повреждения).

Известно ли вам, что между углом вылета мяча и расстоянием (х) от «центральной» точки опорной ногк игрока до стартовой линии мяча (рис. 8) существует зависимость? Мастера футбола хорошо знают это из своего опыта.

Мы не будем здесь рассматривать, как точно определить величину х в зависимости от угла вылета. Скажем только, что расчет показывает, а практика футбола подтверждает одно важное положение—д ля прицельного удара по высоте опорную ногу следует ставить около самой линии, на которой находится мяч. В этом случае траектория мяча будет настильной (отлогой) и мяч не пройдет выше ворот.

Если футболист, изучая технику ударов по воротам, будет правильно ставить опорную ногу и доведет выполнение приема до автоматизма, ему почти не придется переживать неудачу, подобную той, о которой мы рассказывали в начале статьи.

Мы не ставили целью осветить все вопросы движения футбольного мяча. Для этого понадобилась бы большая книга, рассчитанная на читателя, знающего основы механики. Нам хотелось лишь на нескольких примерах показать, как можно использовать законы полета мяча в практике футболиста.

Понимание механики полета мяча помогает игроку более сознательно совершенствоваться в технике ударов и быстрее овладеть спортивным мастерством.

И. СТАНКЕВИЧ, заслуженный мастер спорта